Warehouse Route Optimization

This is a story about how, with considerable design freedom, I solved the Traveling Salesman Problem (TSP) within a warehouse.

Background

The goal of this project was to reduce the walking time when picking up items in a warehouse. We were working with manufacturing companies that had to move various items from the warehouse to the manufacturing area. Walking time can be 60 to 70% of an operator's working time; with optimization, we can greatly increase their productivity. This was to be implemented in ERPNext and written primarily in Python (for the optimizer part), with the UI in Vue.js.

For me, this was a pretty interesting problem to solve. I used to compete in robotics competitions, and when solving, I would think of the competition where the robot rats would have to drive through the maze to find the end. In this case, I was thinking of what instructions would be required for an Amazon robot to navigate through the warehouse to deliver the packages.

So, where did I start?

I originally started searching to see if there was an existing solution, trying to understand the problem space, and at the very least, see how someone else had approached a similar problem. I had initially found a GitHub project named something like "Warehouse Route Optimization xyz lmnop, etc." This was quite a good start, it had defined a few constraints which would be really useful for later. It had divided up the warehouse into Loading Areas where a worker could access items within reaching distance. So, ok, get your robot into reaching distance of the bin, and that seems like it would work. So this was a good start, right? Well, sorta. The solver used was a simple heuristic that would only work on a specific shelf arrangement, think long rows only connected at the top. I would also need to define how the items and bins were stored in this configuration. For me, this wouldn't work.

Work to do

• Figure out how to represent the geometry of a warehouse
• Assign bins to physical locations
• Solve the actual TSP problem

How do you figure out the physical dimensions of a warehouse and where all the bins are located? ERPnext handles the amount of inventory and which bin, but doesn't assign a physical location. I can modify the doctypes to add that data, however.

Ok, and now we need to define the geometry, the physical relationships. We can bring in a 3D scanner and have every measurement down to the mm. Or we could build a virtual copy in a game engine. Or we can measure the shelves, the dimensions of the walkways, etc. But how can we apply a pathing algorithm in any of these cases?

Some Inspiration

I continued my search, this time looking at video games for inspiration. I knew people would want NPCs to travel from one area to the next on a level. I initially found wall riding algorithms, which are used to get characters to move from one area of a map to another quickly while avoiding obstacles. I remember looking at a 3D platformer design with a pathing algorithm and thinking, well, I don't need to solve all of that, but hey, it's quite useful. The thought of jumping between shelves and swinging blades in a warehouse was amusing.

The Solution

This research led me to a much simpler idea. If we could take a floor plan and transform it into a discrete space by dividing it into squares, we could approximate the geometry. We would have walkable and non-walkable areas, or walls and alleys. These squares could be connected by their adjacency and could become a graph object.

The nicest little piece of code of the project, which turns the grid, which is the 2D walkable/non-walkable matrix, into a properly connected graph object.

class Grid_TSP:
    def __init__(self, grid: np.ndarray, scale: float = 1) -> None:
        self.grid = grid
        self.scale = scale
        self.G = nx.Graph()
        self.make_graph()

    def make_graph(self):
        x_shape = self.grid.shape[1]
        for n, pos in enumerate(np.ndindex(self.grid.shape)):
            x = pos[1]
            y = pos[0]
            if self.grid[pos] == 1:
                self.G.add_node(n, pos=(x, -y))
                # Add edged to north and west neighbors if pathway
                if x > 0 and self.grid[y, x - 1] == 1:
                    self.G.add_edge(n, n - 1, weight=self.scale)
                if y > 0 and self.grid[y - 1, x] == 1:
                    north_neighbor = n - x_shape
                    self.G.add_edge(n, north_neighbor, weight=self.scale)

First Map

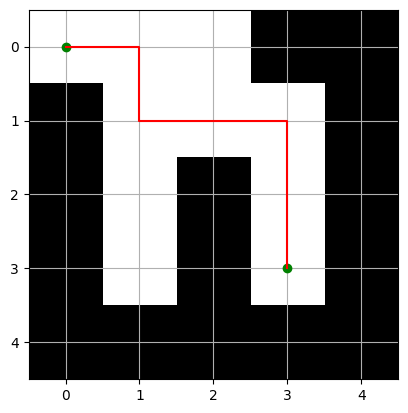
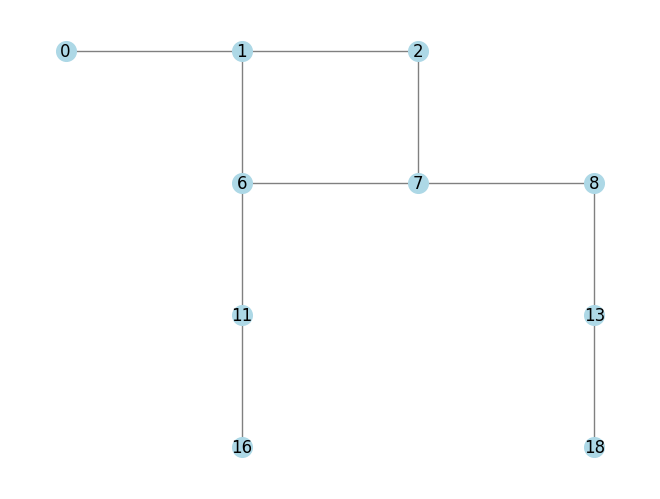
My initial hack was a simple 2D maze. I wanted something that didn't have a straight path. The white is walkable, and the black is non-walkable. And so we can see the physical and graph views side by side.

   

The Second Map

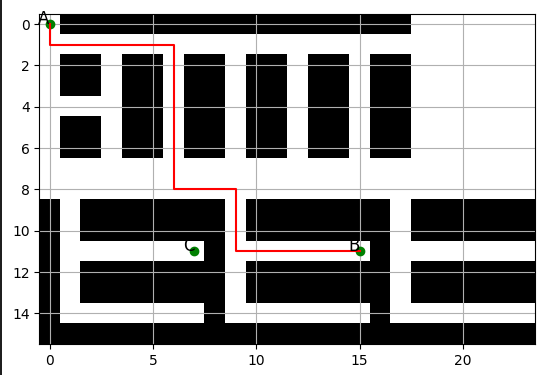
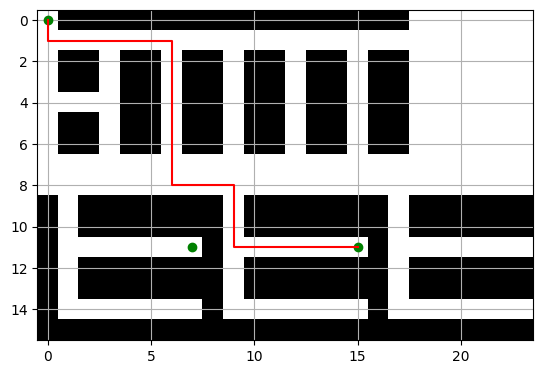
Now, let's make something more complex and realistic. I imagined different storage areas, some shelves in the top section, open storage in the top right, and fridges with shelves in the bottom section. The nodes in the right image, representing the graph object, can represent the out pickup area concept from the initial inspiration. And since we have the physical relationship mapped to a graph, we can use NetworkX traveling_salesman_problem solvers for the pathing part of the problem, sort of. Overall, this is where the project really felt like it was coming together. I have been able to define the geometry and distance between objects, and if I can assign bins to nodes on the graph, I can calculate the shortest route.

   

Testing and Integration

I created some data so that I could assign inventory to bins and bins to nodes. Also, I had to make example pickup lists. I randomly assigned inventory in small quantities so that my pickup lists would have to visit multiple bins. This was a bit of an iterative process, but it was very effective. Also, this data was created and then stored in a static CSV/JSON/parquet format for future testing.

How realistic operations reduced the problem by an order of complexity

The pathing portion was finished; however, the dispatching part was not. Imagine you have to pick up 3 blueberries. There are 2 in a closed bin, 3 in another nearby, and 1 in a far bin. You can pick up 2, then 1 from the stock of 3, or just pick from the stock of 3. Now imagine you also have to pick up strawberries, this now affects your choice for picking up blueberries, which route is the fastest? This problem very quickly becomes a very large combinatorial problem.

Applying rules like FIFO, LIFO, Deplete max bins, Deplete min bins, and excluding the absolute shortest path made this problem much simpler. We could sort the inventory by date or storage levels and reduce the order of complexity. This decision, while it doesn't fulfill the absolute shortest path, still provides a lot of business value.

But I still wanted to solve it, at least a little. My initial strategy was to group the bins into several clusters, and prioritize picking within clusters, and if not, the closest to the pickup/dropoff point. This was honestly a computationally cheap and fairly effective method.

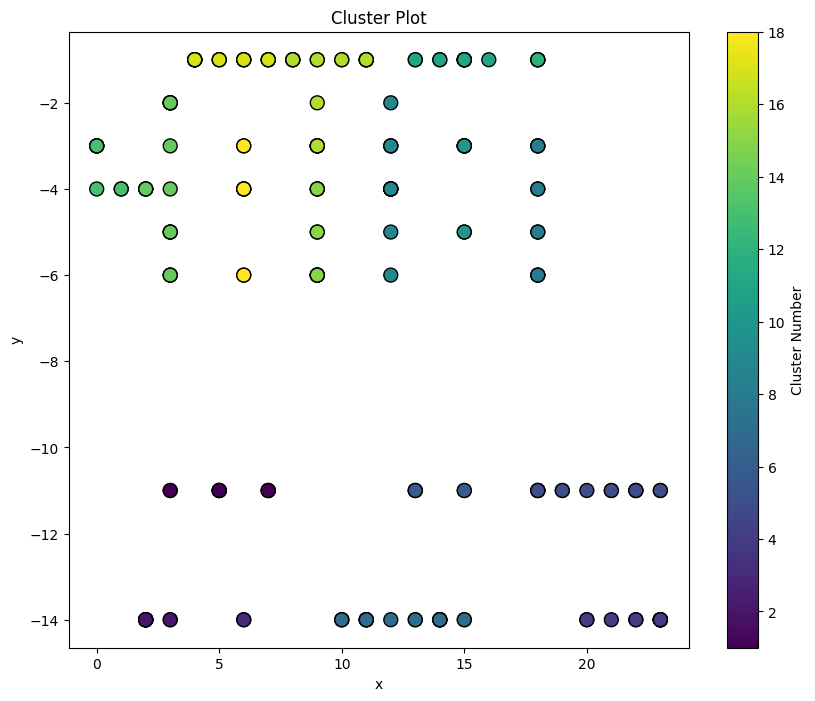
How I would have solved dispatching, looking back

A genetic algorithm with a fitness function to solve the TSP path would have been ideal for solving the dispatching rules and would likely produce a very good solution within a few generations. A genetic algorithm, or possibly constraint programming, would have been useful if considering other constraints that weren't implemented, such as a maximum pickup per trip, fitting 10 things on a cart, or the possibility that some items would have to be picked up by ladder or forklift, requiring more complex routing. These are things that, while they produce a more complete solution, weren't justified.

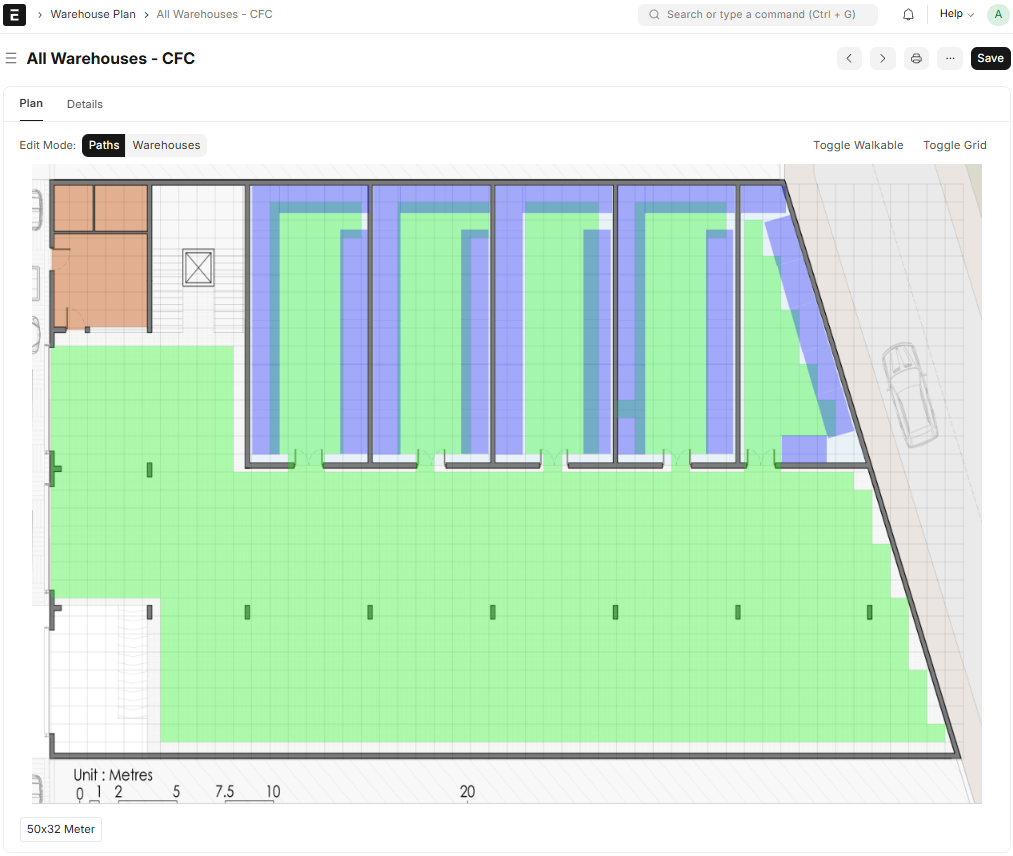
The GUI

This part was sort of pre-imagined. The user uploads a scale image of the floor plan, defines the floor plan into walkable and non-walkable (green), adds the bins (blue), and links them to a near walkable tile. Its simplicity makes it robust; we didn't need 3D scanning tools after all.

Conclusion

I really enjoyed this project as it had a lot of problems to be solved in different areas with an array of possible solutions. It had the potential to be incredibly complex, but with some good engineering judgement, it was kept comparatively simple. Adding location data to items has also had several additional impacts. This was implemented for an electronics manufacturer, where a pick list may be 100 small parts, and if not optimized, walking time can become huge.

All this code is open source MIT-licensed! You can find it here:

• Code
• The ERP implementation

Have questions? Contact me at [email protected]